BARISAN DAN DERET
Di dalam Matematika, sebuah barisan bilangan adalah daftar terurut dari suatu bilangan. Seperti layaknya himpunan, suatu barisan juga memiliki anggota (elemen) yang biasanya disebut suku. Contoh suatu barisan adalah sebagai berikut:
Barisan bilangan bilangan bisa berupa barisan Aritmetika maupun
barisan Geometri. Suku-suku yang berdekatan dari suatu barisan
Aritemetika selalu memiliki selisih yang tetap/konstan, biasa disebut dengan beda. Dalam barisan geometri hasil bagi suku-suku yang saling berdekatan selalu tetap/konstan, yang disebut dengan rasio.
Deret bilangan merupakan penjumlahan suku-suku dari barisan yang
bersesuaian. Contoh deret bilangan yang dibentuk dari barisan-barisan
diatas adalah sebagai berikut:
Deret aritemtika dapat dibentuk dari barisan aritmetika, dan deret geometri dapat diperoleh dari barisan geometri.
Barisan Aritmetika
Barisan aritmetika adalah barisan yang selisih antara suku-suku yang berdekatan tetap/konstan.
Rumus umum suku ke- adalah
adalah 
 adalah
adalah 
dengan  adalah suku awal atau suku pertama dan
adalah suku awal atau suku pertama dan  merupakan selisih suku-suku yang berdekatan.
merupakan selisih suku-suku yang berdekatan.
 adalah suku awal atau suku pertama dan
adalah suku awal atau suku pertama dan  merupakan selisih suku-suku yang berdekatan.
merupakan selisih suku-suku yang berdekatan.
Jumlah angka pada seluruh barisan: 

Barisan Geometri


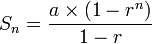
Barisan aritmatika dan deret aritmatika sangat berhubungan, di mana jika suku-suku pada barisannya dijumlahkan, akan membentuk deret.
Ciri umum barisan aritmatika adalah selisih dari setiap suku dengan
suku sebelumnya selalu sama, yang biasa disebut dengan beda atau ‘b’.
Sebagai contoh, 3, 6, 9, 12, … , merupakan barisan aritmatika, karena
selisih dari setiap suku yang berurutan selalu sama, yaitu 6 – 3 = 9 – 6
= 12 – 9 = 3. 3 ini lah yang disebut dengan selisih atau beda (b).
Untuk mencari suku ke-n dari barisan tersebut, dapat digunakan rumus:
Contoh Soal: Tentukan suku ke 11 dari barisan berikut: 11, 18, 25, 32, …
Jawaban:
Perhatikan bahwa 18 – 11 = 25 – 18 = 7, sehingga barisan tersebut merupakan barisan aritmatika, sehingga:
- Deret Aritmatika
Pada deret aritmatika, kita akan menghitung jumlah setiap suku pada barisan tersebut.
Sebagai contoh, 9 + 15 + 21 + 27 + … merupakan deret aritmatika,
karena selisih dari setiap suku yang berurutan selalu sama, yaitu 15 – 9
= 21 – 15 = 6, dan merupakan bentuk penjumlahan.
Untuk mencari jumlah suku-sukunya hingga suku ke-n, dapat kita gunakan rumus:
Contoh Soal: Tentukanlah jumlah dari 17 + 30 + 43 + … + 329.
Jawaban:
Karena selisih setiap suku yang berurutan sama, yaitu 13, dan
berbentuk penjumlahan, maka penjumlahan bilangan tersebut merupakan
deret aritmatika, sehingga dapat kita gunakan rumus 
Akan tetapi, nilai n belum kita ketahui, sehingga harus kita hitung terlebih dahulu dengan menggunakan  seperti pada barisan aritmatika.
seperti pada barisan aritmatika.
Dengan demikian,  = 17 + (n – 1).13 = 329.
= 17 + (n – 1).13 = 329.
17 + 13n – 13 = 329
13n = 329 – 4 = 325
Sumber :












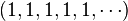

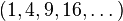

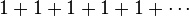

Tidak ada komentar:
Posting Komentar